Pesquisas de intenção de voto e margens de erro
Nos últimos dias temos sido bombardeados por pesquisas de
intenção de voto, elaboradas por diferentes institutos e os resultados
parecem apontar uma única conclusão: não há como prever quem saíra
vencedor das eleições no domingo.
É impossível negar o impacto
causado por esses instrumentos de agregação de preferência, seja
reforçando opiniões, direcionando indecisos ou mesmo causando confusão
generalizada por conta de suas metodologias incompreensíveis para a
maioria da população. Já no primeiro turno causou certa estranheza (e
ótimas piadas sobre a margem de erro!) a diferença entre o que
anunciavam as pesquisas e o que verdadeiramente se viu quando a
população foi às urnas.
Assim, abro espaço para compartilhar o
ótimo texto dos amigos Guilherme Lichand e Raphael Nishimura que juntos
decifram os métodos por trás das pesquisas e traçam uma análise crítica
de seus resultados. Vale a leitura, afinal, toda ajuda é bem-vinda para o
bom exercício democrático!
Ótimo voto a todos brasileiros no domingo!
Pesquisas de intenção de voto e margens de erro
Qual
a importância das pesquisas eleitorais? Para os candidatos, os
resultados ajudam a entender a efetividade do discurso junto a
diferentes estratos do eleitorado e, possivelmente, ajustar esse
discurso para angariar mais votos. Com a ausência de mecanismos
eficientes de consultas populares representativas no Brasil, não é
surpreendente que os candidatos possam aprender sobre as preferências
dos cidadãos mesmo a tão pouco tempo do dia da votação. Sendo assim,
para os eleitores, esse processo pode permitir uma convergência parcial
das propostas para suas preferências. Desde que os compromissos
assumidos em campanha tenham alguma credibilidade, as pesquisas
representariam, portanto, um canal relevante de agregação de
preferências do eleitorado, contribuindo para o melhor funcionamento da
nossa democracia.
Em nenhum momento aqui enfatizamos a capacidade
de previsão dos resultados nas urnas. Vários fatores podem levar a
mudança de comportamento até o dia do pleito, até mesmo porque os
candidatos e os eleitores podem reagir aos tais resultados. O ponto é
que as pesquisas têm valor em si mesmas, como mais uma engrenagem do
processo democrático.
Reconhecida a importância das pesquisas,
torna-se fundamental que esse processo de agregação de preferências
comunique de forma clara e transparente o grau de incerteza nele
contido. Há diversos motivos pelos quais o resultado de uma pesquisa de
opinião pode não expressar perfeitamente as preferências do eleitorado.
De forma grosseira, podemos classificar esses motivos de duas formas:
erros não-amostrais e erros amostrais. Exemplos de erros não-amostrais
são: erros de cobertura, quando parte da população não é abrangida por
uma pesquisa (como pessoas sem acesso a telefone, em uma pesquisa
telefônica); erros de não-resposta, que ocorrem quando indivíduos
selecionados na amostra não respondem à pesquisa, por não serem
encontrados ou por se recusarem a participar; e erros de mensuração,
quando a resposta reportada pelo entrevistado não corresponde com a
realidade, pelos mais diversos motivos. Já os erros amostrais ocorrem
pelo fato de selecionarmos na amostra de uma pesquisa apenas uma fração
da população. Os institutos de pesquisa no Brasil, sob imposição da Lei
n° 9.504, de 30 de setembro de 1997, do Tribunal Superior Eleitoral, são
obrigados a quantificar e divulgar em suas pesquisas apenas os erros
amostrais, sob a forma de uma margem de erro com um determinado nível de
confiança.
A ciência estatística permite compreender e controlar
tais erros amostrais, de forma a garantir que, sob a ausência de erros
não-amostrais, os resultados da pesquisa corresponderão aos da população
dentro uma margem de erro, sob um determinado nível de confiança. Um
ponto de disparidade entre institutos de pesquisa e estatísticos é que,
para o cálculo de tais margens de erro, a teoria estatística
predominante nesses tipos de estudo exige um método de amostragem
probabilístico, em que todos os indivíduos da população possuam uma
probabilidade de serem selecionados conhecida e diferente de zero. No
entanto, alegando que tal método é economicamente inviável - uma vez que
prolongaria muito o período de coleta da amostra -, os institutos
utilizam métodos de amostragem não-probabilísticos - na maioria dos
casos, a chamada amostragem por cotas, em que a seleção dos respondentes
é deixada a critério dos entrevistadores em determinadas áreas
geográficas (muitas vezes selecionadas probabilisticamente) sob
restrições de uma quantidade de entrevistas para diferentes estratos
demográficos da população.
Para muitos estatísticos, o uso de
amostragem não-probabilística não permitiria o cálculo das margens de
erro. Outros estatísticos acreditam que, como em outras áreas de
aplicação da estatística (e mesmo para lidar com erros não-amostrais em
pesquisas), seria possível recorrer a modelos estatísticos para tais
cálculos, que exigiriam fazer certas suposições sobre a forma como a
amostra foi selecionada. A questão central, portanto, é menos sobre a
possibilidade de calcular margens de erro rigorosas para as pesquisas
eleitorais, e mais sobre o que, de fato, os institutos fazem para lidar
com essa preocupação.
Infelizmente, acreditamos que a forma como
os institutos vêm calculando as margens de erros em suas pesquisas não
reflete de forma adequada a coleta de seus dados. Do que é de nosso
conhecimento, os institutos utilizam para esses cálculos um modelo
extremamente simplificado que supõe que os entrevistados tenham sido
diretamente selecionados do eleitorado brasileiro aleatoriamente e com
mesma probabilidade de seleção. As amostras utilizadas pelos institutos
são bem mais complexas do que isso e a margem de erro da pesquisa é
afetada pelo processo de seleção. Por exemplo, em muitos levantamentos
nacionais, a população é estratificada por estado, e em cada um dos
estados é selecionado uma amostra de municípios em um primeiro estágio,
seguindo de uma seleção de segmentos geográficos menores, como blocos ou
ruas, e então domicílios e indivíduos são selecionados pelos
entrevistadores de acordo com critérios demográficos, como sexo, idade e
escolaridade. Para refletir minimamente esse processo, o modelo
utilizado para o cálculo da margem de erro deveria incorporar essas
informações. Isso quer dizer que o problema é ainda mais grave que
ignorar o efeito da amostragem por cotas sobre a margem de erro.
O
processo de estratificação por características sócio demográficas tende
a diminuir a margem de erro, ao permitir que a amostra entrevistada
melhor aproxime a distribuição da população. Já o processo de seleção de
municípios tende a aumentar a margem de erro, uma vez que parte da
variação da intenção de voto é explicada por diferenças entre municípios
(um processo chamado de conglomeração). Para ilustrar a importância de
incorporar esses elementos explicitamente na análise, computamos o
coeficiente que calcula tal efeito de conglomeração para a votação da
candidata Dilma Rousseff para os dois turnos da eleição de 2010 e para o
primeiro turno da eleição de 2014. Entre as duas eleições, o
coeficiente aumentou em mais de 70%, refletindo o maior grau de
polarização regional da eleição atual. Para efeito das pesquisas, isso
significa que, para o mesmo nível de confiança e número médio de
entrevistas por município, seriam necessárias amostras substancialmente
maiores em 2014 para obter a mesma margem de erro, comparativamente a
2010.
Na análise abaixo, mostramos o impacto de incorporar a
conglomeração da população, decorrente da seleção de municípios - sobre a
margem de erro das pesquisas com um método estatístico bastante
simples, utilizando a primeira pesquisa do 2° turno do Datafolha
(Pesquisa BR-01068/2014) e do IBOPE (Pesquisa BR-01071/2014) registradas
no
TSE.
Utilizando
as informações registradas junto ao TSE e calculando o efeito da
conglomeração a partir dos resultados do 1º turno, sumarizamos os
resultados encontrados na tabela abaixo (
link para material complementar).
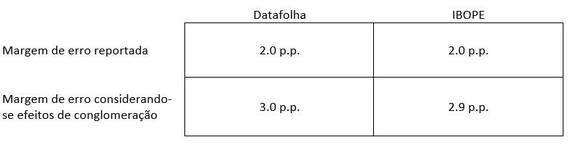
A
tabela mostra que apesar de ambas as pesquisas reportarem margem de
erro de 2%, ambas teriam uma margem de erro próxima a 3% considerando o
efeito de conglomeração do plano amostral. Além disso, nossos cálculos
indicam que para atingir uma margem de erro de 2%, como pretendida,
mantendo-se os mesmos parâmetros das amostras utilizadas pelo DataFolha e
IBOPE, eles precisariam de uma amostra 2,7 vezes maior do que aquela
necessária caso a amostragem fosse probabilística. Infelizmente, não
pudemos calcular o efeito da estratificação em nenhuma das duas
pesquisas, pois não consta na metodologia dos estudos uma informação
necessária para esse cálculo: a distribuição das entrevistas nos
estratos.
Mostramos aqui que a forma como os institutos de
pesquisa eleitoral calculam as margens de erro de suas pesquisas podem
ser inadequadas e há diversas formas de melhorá-las. Utilizamos um
modelo bastante simples que pode ser bem mais aprimorado utilizando-se
outras técnicas estatísticas mais complexas. No entanto, para isso, é
necessário se ter também mais informações sobre o plano amostral e
características da amostra coletada, que a maioria dos institutos não
costumam divulgar. Além dessa falta de transparência dos institutos,
parte do problema é de responsabilidade do TSE, que não exige explicação
sobre a forma como são calculadas as margens de erro, nem qualquer
documentação sobre os modelos e suposições utilizadas para computá-las
ou sobre outras importantes características da amostra, como a
distribuição das entrevistas entre os estratos, necessária para calcular
o efeito da estratificação. Por fim, o TSE exige que a margem de erro
seja divulgada antes mesmo da pesquisa ser coletada, e não obriga os
institutos a atualizarem uma vez concluída a pesquisa, quando se tem
posse de mais informações que permitem um cálculo mais adequado.
Em
função da importância das pesquisas como mecanismo de agregação de
preferências, omitir a verdadeira a margem de erro da pesquisa - assim
como os elementos necessários para que terceiros sejam capazes de
computá-la com precisão - não apenas comunica incompetência mas,
principalmente, prejudica a qualidade da nossa democracia.
Raphael Nishimura (raphael.nishimura@gmail.com) é doutorando em Metodologia de Pesquisa pela universidade de Michigan.
Guilherme
Lichand (guilherme@mgovbrasil.com.br) é doutorando em Economia Política
e Governo pela universidade de Harvard e sócio-fundador da MGov Brasil.
Fonte:http://www.brasilpost.com.br/andre-barrence/pesquisas-e-margens-de-erro_b_6037564.html




